Cómo utilizar el poder del diagrama de Bode para garantizar la estabilidad del circuito

En la década de 1930, Hendrik Wade Bode creó un enfoque intuitivo de ganancia/fase que tenía como único objetivo la estabilidad de un circuito. Esto se convirtió en lo que ahora conocemos como el diagrama de Bode, una representación gráfica intuitiva de la ganancia, la fase y el sistema de realimentación de un circuito o un amplificador en frecuencia.

Dada su utilidad e importancia, tomemos un tiempo para aplicar una técnica de análisis de la estabilidad de Bode para observar la magnitud del factor de realimentación de un circuito y un amplificador de lazo abierto, en decibelios (dB) y respuesta de fase (en grados). En este blog se analizarán estos conceptos y se sugerirá cómo evitar el diseño de un circuito inestable cuando su objetivo principal es la estabilidad de la frecuencia.

Para practicar esta técnica, puede descargar una versión imprimible de un diagrama de Bode de los recursos incluidos en el Manual de innovación de DigiKey en línea.

Diagrama de Bode de polo simple

Con la configuración del circuito de polo simple, las señales de la entrada de voltaje en CC (CC V_IN) pueden ir directamente a la salida de voltaje (V_OUT), mientras que a frecuencias de entrada más altas, la V_OUT es igual a cero decibelios (dB). La creación del diagrama de Bode es sencilla. Las unidades del eje y constituyen la frecuencia logarítmica, y el eje x lineal constituye la ganancia en decibelios o la fase en grados. Hay una gran cantidad de fórmulas que se pueden aplicar al diseñar un diagrama de Bode, pero vayamos al grano con la solución rápida.

La simplicidad del diagrama de Bode radica en que el dibujo de los gráficos solo requiere una herramienta de borde recto y conocer algunas reglas (Figura 1).

Figura 1: Un diagrama de Bode de polo simple que ilustra la magnitud y el cambio de fase utiliza líneas rectas para ilustrar la respuesta de frecuencia y fase del circuito. (Fuente de la imagen: Bonnie Baker)

Los dos diagramas de la Figura 1 representan la frecuencia en comparación con la ganancia y la fase de un par de condensadores/resistencias de polo simple. Los rangos de frecuencia del eje x de los diagramas superior e inferior van de 1 hercio (Hz) a 10 megahercios (MHz). El rango del eje y del diagrama superior es de 0 decibelios (dB) a 100 dB, donde el valor de la señal de 1 Hz es igual a 100 dB. Este valor es coherente con un factor de ganancia de 100,000 x V_IN. La curva azul es la respuesta de ganancia con un polo simple en la f_P o a 100 Hz, donde R es igual a 159 kilohmios (kΩ) y C es igual a 10 nanofaradios (nF).

A medida que la frecuencia sobrepasa la frecuencia del polo (f_P), la curva azul cae a una tasa de -20 dB/década o -6 dB/octava. Esta tasa de atenuación es la primera regla de oro del diagrama de Bode que hay que recordar: Cada polo del circuito cae a una tasa de -20 dB/década, empezando por la frecuencia del polo. Por tanto, si dos polos atenúan la V_OUT en el mismo rango de frecuencia, la tasa de atenuación es de -40 dB/década.

El diagrama inferior de la Figura 1 representa la fase de este circuito de polo simple. A 1 Hz, la fase de la red R/C es de 0 grados (°). A una década antes de la f_P o, en este caso, 10 Hz, la fase del polo simple comienza a caer a una velocidad de -45°/década hacia su objetivo de -90°.

Se aplican varias reglas a la respuesta de fase del polo. La segunda regla de oro del diagrama de Bode para el circuito del polo es que la fase debe ser igual a -45° en la f_P. La tercera y la cuarta regla del diagrama de Bode describen el punto de atenuación y finalización de la fase. La fase del polo simple comienza a caer una década antes de la frecuencia del polo (f_P) y finalmente se estabiliza una década después de la f_P a -90°.

Diagrama de Bode de cero simple

Las reglas del diagrama de Bode de cero simple reflejan lo contrario de las del diagrama de Bode de polo simple. Las posiciones cambian con los mismos valores para R y C para evitar que se produzcan voltajes CC V_IN, mientras se permite que la frecuencia más alta pase por el condensador (Figura 2).

Figura 2: Diagrama de Bode de cero simple que ilustra la magnitud y el cambio de fase. (Fuente de la imagen: Bonnie Baker)

A medida que la frecuencia supera la f_Z, la curva azul se eleva a un ritmo de +20 dB/década. El diagrama inferior de la Figura 2 representa la fase de este circuito de cero simple. A una década antes de la f_Z, la fase de cero simple empieza a elevarse a un ritmo de +45°/década hacia su objetivo de +90°. La fase del circuito cero es igual a +45° en la f_Z.

Para resumir los valores de la Figura 1, la ubicación del polo es f_P, y la magnitud de la ganancia después de f_P tiene una pendiente de -20 dB/década. La fase tiene una pendiente de -45°/década en f_P, comienza su atenuación en 0.1 x f_P y se estabiliza en -90° en 10 x f_P. Para resumir los valores de la Figura 2, la ubicación del cero es f_Z, y la magnitud de la ganancia después de f_Z tiene una pendiente de +20 dB/década. La fase tiene una pendiente de +45°/década en f_Z, comienza su atenuación en 0.1 x f_Z y se estabiliza en +90° en 10 x f_Z.

Diagrama de Bode del amplificador de lazo abierto

El funcionamiento en frecuencia del amplificador operacional (op amp) estándar puede tener varios polos y ceros en la función de transferencia desde los subhercios hasta la frecuencia de corte de cero dB. No hay ningún truco en el diagrama de Bode del amplificador; solo hay que seguir las reglas (Figura 3).

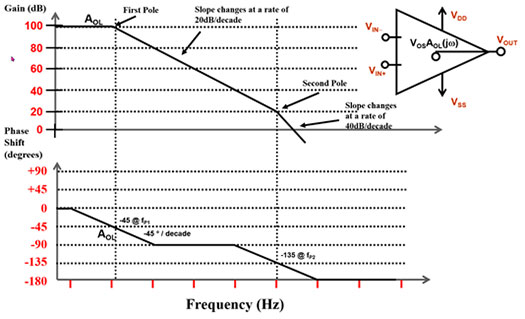Figura 3: Posible diagrama de Bode de un amplificador operacional que ilustra la magnitud y el cambio de fase. (Fuente de la imagen: Bonnie Baker)

La Figura 3 ilustra el ejemplo de un amplificador operacional con dos polos (f₁ y f₂) en la función de transferencia. Con los dos polos, la ganancia cae -20 dB/década cada vez, y la fase cae hasta un total de -180 grados.

En este punto, hemos dado un buen primer paso para aprender a crear diagramas de Bode, pero avancemos hacia el mundo real, donde hay un sistema de realimentación incluido.

Estabilidad del sistema del amplificador de lazo cerrado

Siempre encontrará una red de realimentación rondando si se toma un tiempo para observar los circuitos de un amplificador operacional. La red de realimentación clásica del amplificador operacional cuenta con un elemento directo de ganancia (A_OL(jω)) y un elemento de realimentación (β(jω)).

Figura 4: Red de realimentación clásica del amplificador operacional con un elemento de prealimentación (AOL(jω)) y un elemento de realimentación (β(jω)). (Fuente de la imagen: Bonnie Baker)

En la Figura 4, la ganancia de lazo abierto del amplificador operacional (A_OL) es comparativamente grande, y el factor de realimentación es relativamente pequeño. Esta configuración envía la salida de vuelta al terminal inversor creando una condición de realimentación negativa, en la que esta realimentación pone la salida bajo control. Utilizaremos la inversa de β o 1/β para determinar la estabilidad del circuito de un amplificador operacional.

La forma más fácil de calcular 1/β es colocar una fuente, llamada V_STABILITY, en la entrada no inversora del amplificador operacional. Esta estrategia de cálculo proporcionará una vía excelente para determinar la estabilidad del circuito (Figura 5).

Figura 5: Tanto el circuito de un amplificador operacional no inversor a.) como el circuito de un amplificador operacional inversor b.) tienen una fuente de voltaje ficticia V_STABILITY en su entrada no inversora para permitir que se realice un cálculo preciso del factor 1/β del circuito o ganancia de ruido. (Fuente de la imagen: Bonnie Baker)

Si examina los circuitos de la Figura 5, observará que los circuitos de realimentación que van del terminal no inversor a la salida son los mismos. La ubicación de la fuente de voltaje V_STABILITY permite que se realice un cálculo preciso del factor 1/β del circuito o ganancia de ruido.

En el análisis de la estabilidad de 1/β se usa V_STABILITY. Si se asume que la ganancia de lazo abierto del amplificador operacional es infinita, la función de transferencia de ambos circuitos es igual a:

Ecuación 1

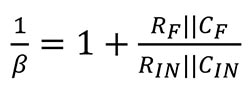Ecuación 2

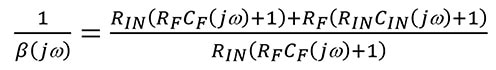Ecuación 3

Cuando el componente de frecuencia de la Ecuación 3, jω, es igual a cero:

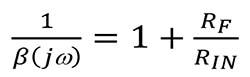Ecuación 4

A medida que jω se acerca al infinito en la Ecuación 3:

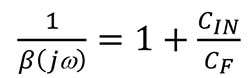Ecuación 5

Las frecuencias para el cero (f_Z) y el polo (f_P) de 1/β son:

Ecuación 6

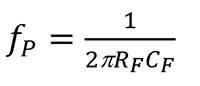Ecuación 7

Los diagramas de Bode de las curvas de análisis de estabilidad de 1/β que cumplen con las reglas establecidas anteriormente se muestran en la Figura 6.

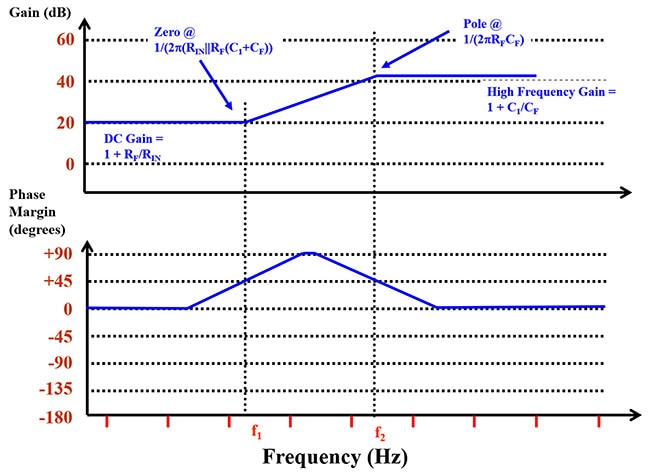Figura 6: La respuesta de frecuencia de 1/β para los ejemplos a.) y b.) de la Figura 5 es idéntica. El cero se da a una frecuencia más baja y el polo, a una frecuencia más alta. (Fuente de la imagen: Bonnie Baker)

La Figura 6 describe la respuesta de frecuencia y fase del 1/β, o ganancia de ruido, del circuito de un amplificador operacional. Esta figura resume las ecuaciones de la 4 a la 7 en forma gráfica. Las ecuaciones 4 y 5 también definen la ganancia de CC y la ganancia de ¥. Y las ecuaciones 6 y 7 identifican el cero y el polo del circuito. Con la información de las Figuras 3 y 6, se proporciona el primer paso para establecer la estabilidad del circuito de un amplificador operacional al definir la función de transferencia del sistema y la ubicación de los polos y ceros. El último paso es superponer las Figuras 3 y 6 en un gráfico.

Determinación de la estabilidad del sistema

La intersección o tasa de cierre de la ganancia de lazo abierto y de lazo cerrado define el cambio de fase del circuito. Generalmente, una tasa de cierre menor o igual a 30 dB indica un circuito estable. Una tasa de cierre superior a 30 dB se acerca a una condición de circuito inestable (Figura 7).

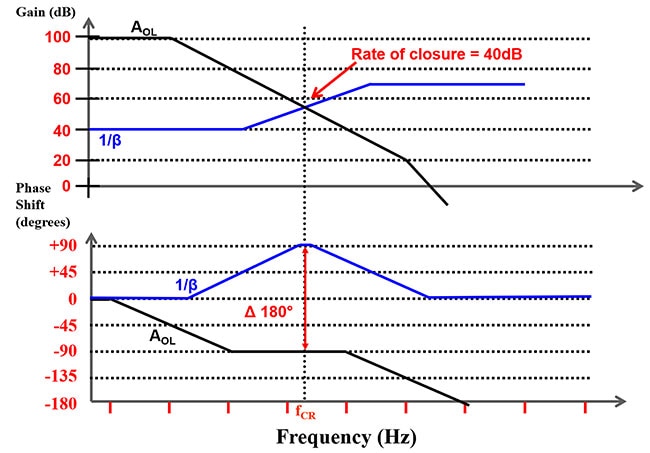Figura 7: Superposición de la respuesta de ganancia y fase de AOL con la respuesta de ganancia y fase de 1/β del amplificador operacional. (Fuente de la imagen: Bonnie Baker)

En la Figura 7, la tasa de cierre entre las curvas de ganancia de A_OL y 1/β es igual a 40 dB. Una tasa de cierre de 40 dB indica un cambio de fase superior a 135°, lo que muestra un circuito inestable. Con esta configuración, la tasa de cierre de 180° produce un circuito que oscila.

Hay muchas soluciones para resolver el problema anterior. Se pueden variar los valores resistivos o capacitivos desplazando las frecuencias del polo y del cero. Otra alternativa es seleccionar un amplificador operacional diferente (Figura 8).

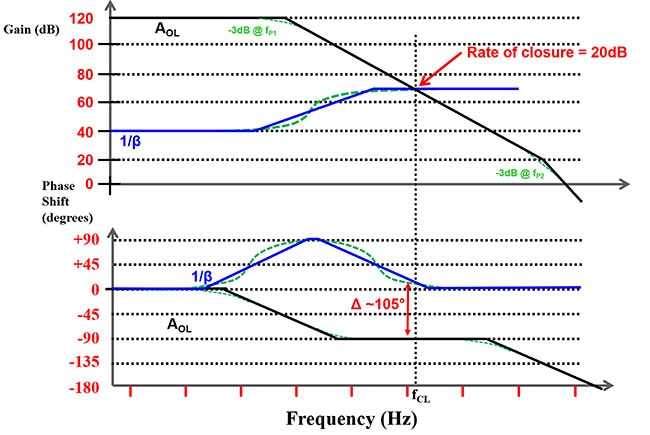Figura 8: Utilizar un amplificador operacional con un ancho de banda mayor que el del amplificador operacional de la Figura 7 sin cambiar las frecuencias del polo y del cero. (Fuente de la imagen: Bonnie Baker)

En la Figura 8, el ancho de banda del amplificador operacional es aproximadamente dos décadas más alto sin un cambio en la red de 1/β. Las líneas verdes discontinuas reflejan los cálculos reales y proporcionan un diagrama de Bode más realista. El aumento del ancho de banda del amplificador cambia la tasa de cierre de 40 dB a 20 dB. El cambio de fase resultante es ahora de aproximadamente 105°, lo que indica un circuito estable.

Las líneas punteadas verdes de la Figura 8 sobrepasan las del diagrama de Bode creado con regla y lápiz al incluir la respuesta del mundo real.

Determinar la ganancia y la fase del circuito

Determinar la ganancia y la fase del circuito de un amplificador requiere un generador de funciones que proporcione la señal de entrada, junto con un analizador de red (Figura 9). A continuación se representa el generador de funciones de barrido analógico con RF de 3 GHz LS3081B de Tabor Electronics.

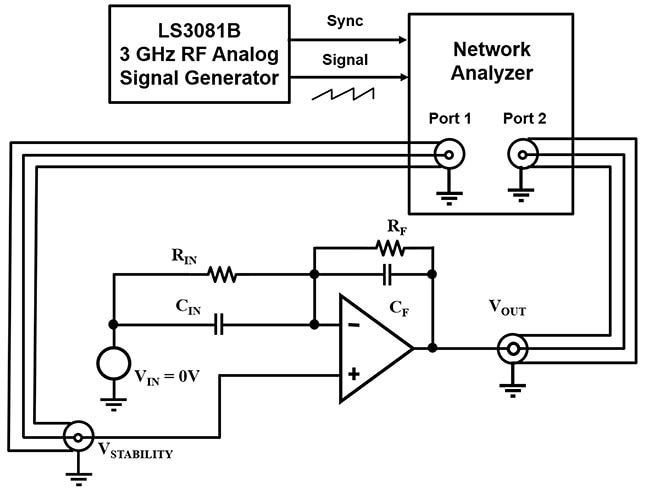Figura 9: Configuración para determinar la ganancia y fase del circuito del amplificador inversor del ejemplo b.) de la Figura 5. (Fuente de la imagen: Bonnie Baker)

En la Figura 9, la aplicación de la señal de entrada del generador de funciones se produce en el puerto 1 en dirección al nodo V_STABILITY. La señal se propaga a través del circuito del amplificador hasta la salida del circuito (V_OUT), donde el analizador de red captura la señal en el puerto 2 y la compara con la señal del puerto 1 del generador de funciones.

Conclusión

Cuando se trata de diseñar circuitos de amplificadores operacionales estables, el diagrama de Bode es una herramienta extremadamente útil que puede agregar a su kit. El poder detrás del diagrama de Bode se hace evidente cuando empieza a analizar los circuitos con varios polos y varios ceros, donde la tasa de cierre entre la ganancia de lazo abierto del amplificador y la red de realimentación define rápidamente la estabilidad de su circuito.

Si bien este blog puede ayudarlo a dominar el uso del diagrama de Bode al mostrarle cómo usar fácilmente una herramienta de borde recto en papel cuadriculado para estimar la ganancia y fase de un circuito de polos y ceros de primer orden, la mejor manera de aprender es practicar. Le recomiendo nuevamente que descargue una versión imprimible de un diagrama de Bode de los recursos incluidos en el Manual de innovación de DigiKey en línea.